[C++] BFS(너비 우선 탐색) vs DFS(깊이 우선 탐색)

BFS(Breath-First Search)

너비 우선 탐색 방식으로 시작 정점으로부터 가까운 정점부터 탐색
큐(Queue)를 이용하여 구현

특징

최단 경로 탐색에 유리
시간복잡도: O(V + E) (V: 정점 수, E: 간선 수)

동작 방식

시작 정점(노드)을 큐에 추가하고 방문했다고 표시
큐에서 정점을 하나 꺼내고, 해당 정점과 연결된 모든 이웃 정점 중 방문하지 않은 정점을 큐에 추가
이 과정을 반복하여 큐가 비면 탐색을 종료

동작 예시

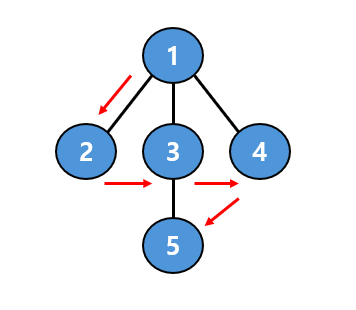
problem_ex

시작 정점: 1
단계별 탐색:
1. 1을 방문하고 큐에 이웃 정점 2, 3, 4를 추가 → 큐: [2, 3, 4]
2. 2를 방문 (큐에서 꺼냄) → 큐: [3, 4]
3. 3을 방문하고 이웃 정점 5를 추가 → 큐: [4, 5]
4. 4를 방문 → 큐: [5]
5. 5를 방문 → 큐: []
최종 탐색 순서: 1 → 2 → 3 → 4 → 5

BFS 구현 흐름

void bfs(int start) {
    queue<int> q;
    q.push(start);          // 시작 정점을 큐에 추가
    visited[start] = true;  // 시작 정점 방문 표시

    while (!q.empty()) {    // 큐가 빌 때까지 반복
        int current = q.front();
        q.pop();
        cout << current << " "; // 현재 정점 출력

        for (int next : graph[current]) {
            if (!visited[next]) {
                q.push(next);   // 이웃 정점을 큐에 추가
                visited[next] = true;
            }
        }
    }
}

BFS 전체 코드

#include <iostream>
#include <queue>
#include <vector>

using namespace std;

vector<int> graph[1001];
bool visited[1001]; // 방문 여부 체크

void bfs(int start) {
    queue<int> q;
    q.push(start);
    visited[start] = true;

    while (!q.empty()) {
        int current = q.front();
        q.pop();
        cout << current << " "; 

        for (int next : graph[current]) {
            if (!visited[next]) {
                q.push(next);
                visited[next] = true;
            }
        }
    }
}

int main() {
    int n, m, start;
    cin >> n >> m >> start; // 정점 수, 간선 수, 시작 정점 입력

    // 간선 입력
    for (int i = 0; i < m; i++) {
        int u, v;
        cin >> u >> v;
        graph[u].push_back(v);
        graph[v].push_back(u); // 무방향 그래프
    }

    bfs(start);

    return 0;
}

BFS 문제

최단 경로 문제(Shortest Path Problem)
- BFS는 가장 가까운 노드부터 탐색하므로, 그래프에서 두 노드간의 최단 경로를 찾는 문제에 유리
  - 미로 찾기: 미로의 출발 지점에서 목표지점까지 최단 경로를 찾아라
  - 그래프에서의 최단 경로 탐색: 간선의 가중치가 모두 1인 그래프에서 두 정점간의 최단 경로를 찾아라

DFS(Depth-First Search)

깊이 우선 탐색 방식으로 한 경로를 끝까지 탐색한 후, 다른 경로를 탐색하는 방식
재귀(Recursion) 또는 스택(Stack)를 이용하여 구현

특징

경로 탐색(모든 경우의 수 탐색)에 유리
시간복잡도: O(V + E) (V: 정점 수, E: 간선 수)

동작 방식

시작 정점(노드)을 스택에 추가하고 방문했다고 표시
스택에서 정점을 하나 꺼내고, 해당 정점과 연결된 방문하지 않은 이웃 정점이 있다면 스택에 추가하고 계속 깊이 탐색
더 이상 방문할 이웃 정점이 없으면 스택에서 정점을 꺼내면서 되돌아감
모든 정점을 방문할 때 까지 반복

동작 예시

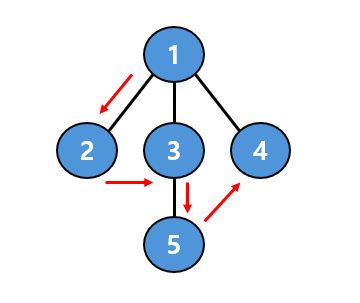
problem_ex

시작 정점: 1
단계별 탐색:
1. 1을 방문하고, 이웃 정점 2, 3, 4를 스택에 추가 → 스택: [4, 3, 2]
2. 2를 방문하고 더 이상 갈 곳이 없으므로 되돌아감 → 스택: [4, 3]
3. 3을 방문하고, 이웃 정점 5를 스택에 추가 → 스택: [4, 5]
4. 5를 방문하고 더 이상 갈 곳이 없으므로 되돌아감 → 스택: [4]
5. 4를 방문하고 더 이상 갈 곳이 없으므로 되돌아감 → 스택: []
최종 탐색 순서: 1 → 2 → 3 → 5 → 4

1단계에서 2보다 4가 먼저 탐색될시

DFS는 스택(Last In First Out) 자료구조를 사용하기 때문에 이웃 정점을 스택에 추가할 때 나중에 추가된 정점이 먼저 탐색된다.
따라서 이웃 정점을 추가할 때 순서를 조심해야 하는데,
- 오름차순 탐색: 이웃 정점을 오름차순으로 탐색하고 싶다면, 내림차순으로 스택에 추가
- 내림차순 탐색: 반대로 내림차순으로 탐색하고 싶다면, 오름차순으로 스택에 추가

DFS 구현 흐름

void dfs(int current) {
    visited[current] = true;  // 현재 정점 방문 표시
    cout << current << " ";   // 현재 정점 출력

    for (int next : graph[current]) {
        if (!visited[next]) {
            dfs(next);         // 재귀 호출로 이웃 정점 탐색
        }
    }
}

DFS 전체 코드(재귀)

#include <iostream>
#include <vector>

using namespace std;

vector<int> graph[1001];
bool visited[1001];

void dfs(int current) {
    visited[current] = true;
    cout << current << " "; // 현재 정점 출력

    for (int next : graph[current]) {
        if (!visited[next]) {
            dfs(next);
        }
    }
}

int main() {
    int n, m, start;
    cin >> n >> m >> start; // 정점 수, 간선 수, 시작 정점 입력

    // 간선 입력
    for (int i = 0; i < m; i++) {
        int u, v;
        cin >> u >> v;
        graph[u].push_back(v);
        graph[v].push_back(u); // 무방향 그래프
    }

    dfs(start);

    return 0;
}

DFS 전체 코드(스택)

#include <iostream>
#include <vector>
#include <stack>

using namespace std;

vector<int> graph[1001];
bool visited[1001];

void dfs_stack(int start) {
    stack<int> s;
    s.push(start);
    visited[start] = true;

    while (!s.empty()) {
        int current = s.top();
        s.pop();
        cout << current << " "; // 현재 정점 출력

        for (int next : graph[current]) {
            if (!visited[next]) {
                s.push(next);
                visited[next] = true;
            }
        }
    }
}

int main() {
    int n, m, start;
    cin >> n >> m >> start; // 정점 수, 간선 수, 시작 정점 입력

    // 간선 입력
    for (int i = 0; i < m; i++) {
        int u, v;
        cin >> u >> v;
        graph[u].push_back(v);
        graph[v].push_back(u); // 무방향 그래프
    }

    dfs_stack(start);

    return 0;
}

DFS 문제

경로 찾기 문제(Path Finding Problem)
- DFS는 깊이 우선 탐색을 하며 한 경로를 끝까지 탐색하는 방식이기 때문에 특정 경로를 찾거나 모든 경로를 탐색하는 문제에 유리
  - 미로에서 출구찾기: 미로에서 출구까지 가는 경로가 존재하는지 확인하라
  - 그래프에서 모든 경로 탐색: 주어진 시작 정점에서 목표 정점까지 강 수 있는 모든 경로를 찾아라
백트래킹 문제(Backtracking)
- 모든 가능한 경우를 탐색하는데 유용
- 조건을 만족하지 않으면 되돌아가며 탐색을 계속하기 때문에 백트래킹 문제에 적합
  - 조합 생성: 주어진 수들 중에서 특정 조건을 만족하는 모든 조합을 찾아라
  - 순열 생성: 주어진 수들로 가능한 모든 순열을 만들어라
그래프의 사이클 탐지(Cycle Detection)
- 탐색중에 방문한 노드를 다시 방문하는지 체크하여 사이클을 탐지할 수 있다
  - 방향 그래프에서 사이클 찾기
  - 무방향 그래프에서 사이클 찾기
트리의 구조 탐색
- 이진 트리의 후위 순회/전위 순회/중위 순회 탐색

yoon0722

BFS(Breath-First Search)

특징

동작 방식

동작 예시

BFS 구현 흐름

BFS 전체 코드

BFS 문제

DFS(Depth-First Search)

특징

동작 방식

동작 예시

1단계에서 2보다 4가 먼저 탐색될시

DFS 구현 흐름

DFS 전체 코드(재귀)

DFS 전체 코드(스택)

DFS 문제